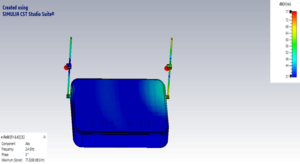
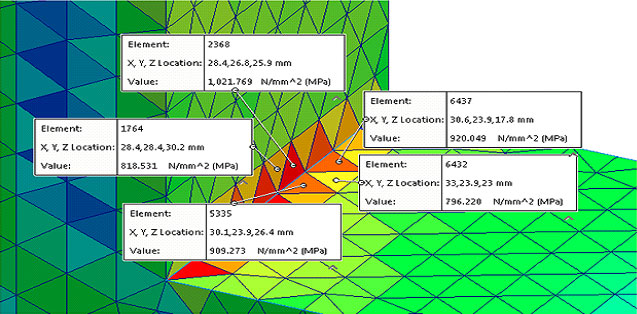
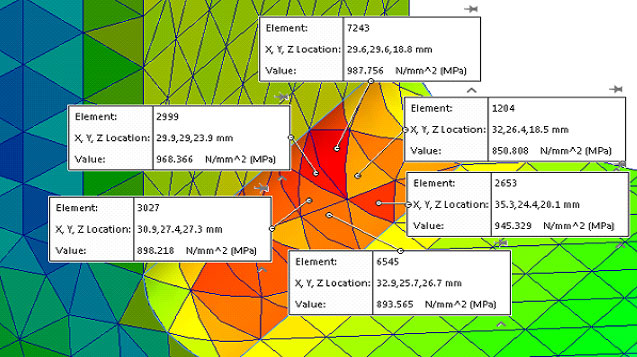
A stress singularity is a point of the mesh where the stress does not convergence towards a specific value. The more we refine the mesh, the stress at this point keeps increasing. Theoretically, the stress at the singularity is infinite. It is important to identify these singularities and differentiate from desired stresses. The sharp corners, point loads, fixtures on edges can cause singularities to develop. The problem of stress singularity is inherent in all finite element analysis and very simple to troubleshoot. A distinctive behavior of a stress singularity is the increasing stress value with respect to increasing mesh refinement as shown below.
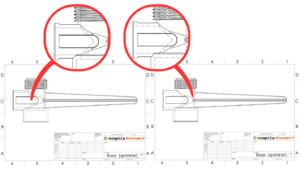
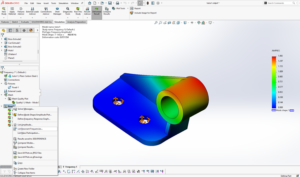
Diverging stresses near sharp corner as the mesh gets refined is indication of stress singularities
To differentiate stress singularities from true stress concentrations, refine the mesh either globally or locally at the regions where stress hot spots are detected. When you rerun the stress hot spot diagnostics tool, the areas of stress concentrations should be filtered out, and the remaining stress hot spots would point to stress singularities. However, in the physical world, stress singularities do not occur as the material will yield or crack when stresses exceed the material’s ultimate strength limit.
Irregular Stress distribution at Sharp corners
Smooth stress distribution at fillet corner
Add fillets to sharp edges and “round off” the corners at the locations where high stress gradients appear. The fillets distribute the stress over a broader area and effectively increase the load bearing capacity of parts. In a Physical world, a manufactured “sharp corner” will always have small fillet radius.
Applying loads on vertices or along edges should be avoided, if possible. Distribute the load to areas on the model to approximate as accurately as possible in the real loading conditions. Even if the load is applied as a singular point load creating a stress singularity (σ = P/A and A=0 → σ=∞), the stress distribution at some distance away from the load applied will still be correct. This is based on the St. Venant’s principle that states that the difference between the effects of two different but statically equivalent loads becomes very small at sufficiently large distances from the load.
The Stress singularities can contaminate stress distributions only locally. If the stress singularities appear in the region which is of no interest for you, then it may be ignored and continue probing the stress results further away which should remain ” uncontaminated “.